|
Abstract:
By introducing k-marked Durfee symbols, Andrews found a combinatorial
interpretation of 2k-th symmetrized moment η2k(n)
of ranks of partitions of n in terms
of (k + 1)-marked Durfee symbols of n. In this paper, we consider the k-th symmetrized
positive moment 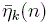 of ranks of partitions of n
which is defined as the truncated sum
over positive ranks of partitions of n. As combintorial interpretations of of ranks of partitions of n
which is defined as the truncated sum
over positive ranks of partitions of n. As combintorial interpretations of
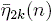 and and
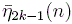 , we show that for given k and i with
1 ≤ i ≤ k + 1, , we show that for given k and i with
1 ≤ i ≤ k + 1, 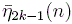 equals the number
of (k + 1)-marked Durfee symbols of n with the i-th rank being zero and equals the number
of (k + 1)-marked Durfee symbols of n with the i-th rank being zero and
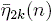 equals
the number of (k + 1)-marked Durfee symbols of n with the i-th rank being positive.
The interpretations of equals
the number of (k + 1)-marked Durfee symbols of n with the i-th rank being positive.
The interpretations of 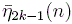 and and
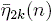 are independent of i,
and they imply the interpretation of η2k(n) given
by Andrews since η2k(n) equals are independent of i,
and they imply the interpretation of η2k(n) given
by Andrews since η2k(n) equals
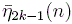 plus twice of plus twice of
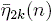 . Moreover, we obtain the
generating functions of . Moreover, we obtain the
generating functions of 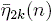 and and
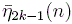 . .
AMS Classification:
05A17, 11P83, 05A30.
Keywords:
rank of a partition, k-marked Durfee symbol, moment of ranks
Download:
pdf
|