|
Abstract:
A family of k-subsets A1, A2,... ,
Ad on [n] = {1, 2,... , n} is called a (d, c)-cluster
if the union A1 ∪A2 ∪...∪Ad
contains at most ck elements with c < d.
Let F be a family of k-subsets
of an n-element set. We show that for k ≥ 2 and n ≥
k+ 2, if every
(k, 2)-cluster of F is intersecting, then F contains no (k- 1)-dimensional
simplices. This leads to an affirmative answer to Mubayi's conjecture for
d = k based on Chvatal's simplex theorem. We also show that for any
d satisfying 3 ≤ d ≤ k and n ≥
AMS Classification: 05D05 Keywords: clusters of subsets, Chvátal's simplex theorem, d-simplex, Erdös- Ko-Rado Theorem Download: pdf |
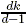 , if every (d,
, if every (d,
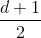 )-cluster is intersecting,
then |F| ≤
)-cluster is intersecting,
then |F| ≤ 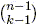 with equality only when F is a complete star.
This result is an extension of both Frankl's theorem and Mubayi's
theorem.
with equality only when F is a complete star.
This result is an extension of both Frankl's theorem and Mubayi's
theorem.