|
Abstract: In this paper, we use the
Riemann zeta function ζ(x) and the Bessel zeta function
ζμ(x) to study the log-behavior of combinatorial
sequences. We prove that ζ(x) is log-convex for x>1. As a
consequence, we deduce that the sequence {|B2n|/(2n)!}n≥ 1 is
log-convex,
where Bn is the n-th Bernoulli number.
We introduce the function θ(x)=(2ζ(x)Γ(x+1))1/x,
where Γ(x) is the gamma function, and we show that
logθ(x) is strictly increasing for x≥6.
This confirms a conjecture of Sun stating that the sequence
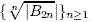 is strictly increasing.
Amdeberhan, Moll and Vignat defined the numbers
an(μ)=22n+1(n+1)!(μ+1)nζμ(2n) and
conjectured that the sequence {an(μ)}n≥ 1 is
log-convex for μ=0 and μ=1. By proving that
ζμ(x) is log-convex
for x>1 and μ>-1, we show that the sequence
{an(μ)}n≥1 is log-convex for any μ>-1. We
introduce another function θμ(x) involving
ζμ(x) and the gamma function Γ(x) and we
show that logθμ(x) is strictly increasing for
x>8e(μ+2)2. This implies that is strictly increasing.
Amdeberhan, Moll and Vignat defined the numbers
an(μ)=22n+1(n+1)!(μ+1)nζμ(2n) and
conjectured that the sequence {an(μ)}n≥ 1 is
log-convex for μ=0 and μ=1. By proving that
ζμ(x) is log-convex
for x>1 and μ>-1, we show that the sequence
{an(μ)}n≥1 is log-convex for any μ>-1. We
introduce another function θμ(x) involving
ζμ(x) and the gamma function Γ(x) and we
show that logθμ(x) is strictly increasing for
x>8e(μ+2)2. This implies that
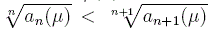 for n>
4e(μ+2)2. Based on Dobinski's formula, we prove that for n>
4e(μ+2)2. Based on Dobinski's formula, we prove that
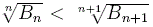 for n≥1, where
Bn is the n-th
Bell number. This confirms another conjecture of Sun.
We also establish a connection between
the increasing property of for n≥1, where
Bn is the n-th
Bell number. This confirms another conjecture of Sun.
We also establish a connection between
the increasing property of 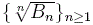 and
Hölder's inequality in probability theory. and
Hölder's inequality in probability theory.
AMS Classification: 05A20, 11B68
Keywords:
log-convexity, Riemann zeta function, Bernoulli number, Bell
number, Bessel zeta function, Narayana number
Download: PDF
|