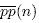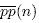Abstract:   Bringmann and Lovejoy introduced a rank for overpartition pairs and investigated its role in congruence properties of  , the number of overpartition pairs of n. In particular, they applied the theory of Klein forms to show that there exist many Ramanujan-type congruences for  . In this paper, we derive two Ramanujan-type identities and some explicit congruences for 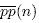  . Moreover, we find three ranks as combinatorial interpretations of the fact that 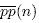  is divisible by three for any n. 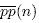We also construct infinite families of congruences for   modulo 3 and 5, and two congruence relations modulo 9.

  AMS Classification :   05A17, 11P83

  Keywords:   overpartition pairs, rank of overpartition pairs, congruence, sum of squares

  Download:  pdf