W.Y.C. Chen, Q.-H. Hou and H.-T. Jin,
The Abel-Zeilberger algorithm,
Electron. J. Combin. 18(2) (2011) #P17.

Cited by

  1. G. Cardona, A. Mir and F. Rosselló, The expected value under the Yule model of the squared path-difference distance, Appl. Math. Lett. 25 (2012) 2031-2036.

  2. D.K. Du, Q.-H. Hou and H.-T.Jin, Non-commutative elimination proves special number identities, Preprint.

  3. H.-T. Jin and D.K. Du, Abel's lemma and identities on harmonic numbers, Integers, 15 (2015) Paper No. A22, 11 pp.

  4. S.I. Kalmykov and D.B. Karp, Log-convexity and log-concavity for series in gamma ratios and applications, J. Math. Anal. Appl. 406 (2013) 400-418.

  5. H. Moll, Numbers and Functions, AMS, Providence, 2012.

  6. C.P. Niculescu and M.M. Stanescu, A note on Abel's partial summation formula, Aequat. Math. 91(6) (2017) 1009-1024.

  7. R.-H. Wang, Rational reductions for holonomic sequences, arXiv:2401.15887.

  8. J. Wang and C. Wei, Derivative operator and summation formulae involving generalized harmonic numbers, J. Math. Anal. Appl. 434 (2016) 315-341.

  9. J. Wang and C. Wei, Four families of summation formulas involving generalized harmonic numbers, Ramanujan J. 45 (2018) 73-94.

  10. Y.P. Wang and X. Tong, Several identities involving q-harmonic numbers by q-Chu-Vandermonde convolution formula, Ars Combin. 122 (2015) 21-32.

  11. C. Wei, Minton-Karlsson identities and summation formulae involving generalized harmonic numbers, Integral Transforms Spec. Funct. 27 (2016) 592-598.

  12. C. Wei, D.X. Gong and L.L. Liu, Summation formulas involving harmonic numbers with even or odd indexes, arXiv:1806.09985.

  13. C. Wei, D.X. Gong and Q. Wang, Chu–Vandermonde convolution and harmonic number identities, Integral Transforms Spec. Funct. 24 (2013) 324-330.

  14. C. Wei, D.X. Gong and Q.L. Yan, Telescoping method, derivative operators and harmonic number identities, Integral Transforms Spec. Funct. 25 (2014) 203-214.

  15. C. Wei and Q. Wang, A Saalschütz-type identity and summation formulae involving generalized harmonic numbers, J. Math. Anal. Appl. 449(2) (2017) 1036-1052.

  16. C. Wei and X.X. Wang, Summation formulas involving generalized harmonic numbers, J. Difference Equ. Appl. 22(10) (2016) 1554-1567.

  17. C. Wei and X.X. Wang, Whipple-type 3F2-series and summation formulae involving generalized harmonic numbers, Int. J. Number Theory 14(9) (2018) 2385-2407.

  18. C. Wei, Q.L. Yan and D.X. Gong, A family of summation formulas involving generalized harmonic numbers, arXiv:1203.2863.

  19. C. Wei, Q.L. Yan and D.X. Gong, A family of summation formulae involving harmonic numbers, Integral Transforms Spec. Funct. 26(9) (2015) 667-677.

  20. C. Wei, Y.B. Yu and H.J. Zhang, Watson-type 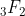-series and summation formulae involving generalized harmonic numbers, J. Difference Equ. Appl. 24(9) (2018) 1444-1472.

  21. Q.L. Yan and Y.Q. Liu, Harmonic number identities involving telescoping method and derivative operator, Integral Transforms Spec. Funct. 28(10) (2017) 703-709.