|
Abstract: Hirschhorn and Sellers studied arithmetic
properties of the number of partitions with odd parts distinct. In
another direction, Hammond and Lewis investigated arithmetic
properties of the number of bipartitions. In this paper, we consider
the number of bipartitions with odd parts distinct. Let this number
be denoted by pod-2(n). We obtain two Ramanujan type
identities for pod-2(n), which imply that pod-2(2n+1) is
even and pod-2(3n+2) is divisible by 3. Furthermore, we show
that for any α ≥ 1 and
n ≥ 0, pod-2 AMS Classification: 05A17, 11P83 Keywords: partition, bipartition, congruence, birank Download: pdf |
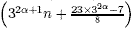 is a multiple of 3 and
pod-2
is a multiple of 3 and
pod-2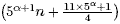 is divisible by 5. We also find combinatorial interpretations for
the two congruences modulo 2 and 3.
is divisible by 5. We also find combinatorial interpretations for
the two congruences modulo 2 and 3.