M.A. Abdlhusein, The Euler operator for basic hypergeometric series, Int. J. Adv. Appl. Math. Mech. 2 (2014) 42-52.
M.A. Abdlhusein, The generalized Hahn polynomials, TWMS J. Appl. Eng. Math. 5 (2015) 231-248.
M.A. Abdlhusein, The new application of the Cauchy operator, Journal of Zankoi Sulaimani, Part-A (2015) 193-204.
M.A. Abdlhusein, Two operator representations for the trivariate q-polynomials and Hahn polynomials, Ramanujan J. 40 (2016) 491-509.
I. Ahmed,
A study of Hermite polynomials and its generalizations,
Master Thesis, Aligarh Muslim University, 2008.
S.A. Ali and A. Agnihotri, A new summation formula for 2ψ2 basic bilateral hypergeometric series by q-exponential
operator technique, Advanced Studies in Contemporary Mathematics 29(3) (2019) 331-338.
S.A. Ali and A. Agnihotri, Certain basic hypergeometric series identities through q-exponential operator technique, International Bulletin of Mathematical Research 1 (2014) 49-53.
S.A. Ali and A. Agnihotri, Parameter augmentation for basic hypergeometric series by Cauchy operator, Palest. J. Math. 6 (2017) 159-164.
J. Cao, New proofs of generating functions for Rogers–Szegö polynomials, Appl. Math. Comput. 207 (2009) 486-492.
J. Cao, Bivariate generating functions for Rogers–Szegö polynomials, Appl. Math. Comput. 217 (2010) 2209-2216.
J. Cao, Notes on Carlitz's q-operators, Taiwanese J. Math. 14 (2010) 2229-2244.
J. Cao, Alternative proofs of generating functions for Hahn polynomials and some applications, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 14 (2011) 571-590.
J. Cao, Moments for generating functions of Al-Salam-Carlitz polynomials, Abstr. Appl. Anal. (2012) Art. ID 548168, 18 pp.
J. Cao, A note on q-integrals and certain generating functions, Stud. Appl. Math. 131 (2013) 105-118.
J. Cao, q-Difference equations for generalized homogeneous q-operators and
certain generating functions, J. Difference Equ. Appl. 20 (2014) 837-851.
J. Cao, A note on generalized q-difference equations for
<q-beta and Andrews–Askey integral, J. Math. Anal. Appl. 412 (2014) 841-851.
J. Cao and Z.-H. Shen, On q-integral representations for
q-Hahn and Askey-Wilson polynomials and certain generating functions, Appl. Math. E-Notes 17 (2017) 186-198.
J. Cao and X.-L. Zhao, Exponential operator decomposition for Carlitz type generating functions, Ars Combin. 116 (2014) 245-255.
W.Y.C. Chen and A.M. Fu, Cauchy augmentation for basic hypergeometric series, Bull. London Math. Soc. 36 (2004) 169-175.
W.Y.C. Chen, A.M. Fu and B.Y. Zhang, The homogeneous q-difference operator, Adv. in Appl. Math. 31 (2003) 659-668.
W.Y.C. Chen, H.L. Saad and L.H. Sun, The bivariate Rogers-Szegö polynomials, J. Phys. A 40 (2007) 6071-6084.
W.Y.C. Chen, H.L. Saad and L.H. Sun, An operator approach to the Al-Salam–Carlitz polynomials, J. Math. Phys. 51 (2010) 043502, 13 pp.
V.Y.B. Chen and N.S.S. Gu, The Cauchy operator for basic hypergeometric series, Adv. in Appl. Math. 41 (2008) 177-196.
T. Ernst, The history of q-calculus and a new method, Department of Mathematics, Uppsala University, 2000.
J.-P. Fang, q-Differential operator identities and applications, J. Math. Anal. Appl. 332 (2007) 1393-1407.
J.-P. Fang, Remarks on a generalized q-difference equation, J. Difference Equ. Appl. 21 (2015) 934-953.
J.-P. Fang, Generalizations of Milne's ) q-Chu-Vandermonde summation,
Czechoslovak Math. J. 66(141) (2016) 395-407.
q-Chu-Vandermonde summation,
Czechoslovak Math. J. 66(141) (2016) 395-407.
J. Gao, B.B. Xu, S. Arjika, A note on generalized q-difference equations for general al-salam–carlitz polynomials, arXiv:2011.05848v1.
V.J.W. Guo, Elementary proofs of some q-identities of Jackson and Andrews–Jain, Discrete Math. 295 (2005) 63-74.
Z.Y. Jia, Two new q-exponential operator identities and their applications, J. Math. Anal. Appl. 419 (2014) 329-338.
Z.Y. Jia, A new extension of the nonterminating 6φ5 summation via q-difference equation,
Taiwanese J. Math., to appear.
C. Krattenthaler and K.S. Rao, Automatic generation of hypergeometric identities by the beta integral method, J. Comput. Appl. Math. 160 (2003) 159-173.
A. Kumar, M.S. Khan and K.P. Yadav, Parameter augmentation for some basic hypergeometric series identities, J. Math. Comput. Sci. 2 (2012) 1532-1538.
N.N. Li and W. Tan, Two generalized q-exponential operators and their applications, Adv. Difference Equ. (2016) Paper No. 53, 14 pp.
Z.-G. Liu, Some operator identities and q-series transformation formulas, Discrete Math. 265 (2003) 119-139.
Z.-G. Liu, An identity of Andrews and the Askey-Wilson integral, Ramanujan J. 19 (2009) 115-119.
Z.-G. Liu, Two q-difference equations and
q-operator identities, J. Difference Equ. Appl. 16 (2010) 1293-1307.
Z.-G. Liu, An extension of the non-terminating 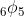 summation and the Askey–Wilson polynomials, J. Difference Equ. Appl. 17 (2011) 1401-1411.
summation and the Askey–Wilson polynomials, J. Difference Equ. Appl. 17 (2011) 1401-1411.
Z.-G. Liu, On the q-partial differential equations and
q-series, In: The Legacy of Srinivasa Ramanujan, 213-250,
Ramanujan Math. Soc. Lect. Notes Ser. 20, Ramanujan Math. Soc. Mysore, 2013.
Z.-G. Liu and J. Zeng, Two expansion formulas involving the Rogers–Szegö polynomials with applications, Int. J. Number Theory 11 (2015) 507-525.
D.-Q. Lu, q-difference equation and the Cauchy operator identities, J. Math. Anal. Appl. 359 (2009) 265-274.
Y.-P. Mu, Parameter augmentation and the q-Gosper algorithm, J. Symbolic Comput. 43 (2008) 874-882.
K.N. Murthy, A study of the theory of basic hypergeometric series and allied topics, Ph.D. Thesis, University of Mysore, 2013.
H.L. Saad and M.A. Abdlhusein, The q-exponential operator and generalized Rogers-Szegö polynomials,
J. Adv. Math. 8 (2014) 1440-1455.
H.L. Saad and F.A. Reshem, The operator ) for the polynomials
for the polynomials
) , Journal of Advances in Mathematics 9 (2015) 2888-2904.
, Journal of Advances in Mathematics 9 (2015) 2888-2904.
H.L. Saad and A.A. Sukhi, The q-exponential operator, Appl. Math. Sci. 7 (2005) 6369-6380.
H.M. Srivastava and M.A. Abdlhusein, New forms of the Cauchy operator and some of their applications, Russ. J. Math. Phys. 23 (2016) 124-134.
M.J. Wang, A generalization of the q-Pfaff-Saalschütz formula, Contrib. Discret. Math. 3 (2008) 25-30.
M.J. Wang, Generalizations of Milne's ) q-binomial theorems, Comput. Math. Appl. 58 (2009) 80-87.
q-binomial theorems, Comput. Math. Appl. 58 (2009) 80-87.
M.J. Wang, q-integral representation of the Al-Salam-Carlitz polynomials,
Appl. Math. Lett. 22 (2009) 943-945.
C.H. Zhang, Parameter augmentation for two formulas, Electron. J. Combin. 13 (2006) Note 19, 5 pp.
C.H. Zhang and Z.Z. Zhang, Extensions of two q-series identities,
Adv. Stud. Contemp. Math. (Kyungshang) 13 (2006) 81-85.
Z.Z. Zhang, Some 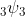 transformations formulas related to Bailey's
transformations formulas related to Bailey's
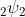 , Ars Combin. 78 (2006) 257-265.
, Ars Combin. 78 (2006) 257-265.
Z.Z. Zhang, Operator identities and several ) generalizations of the Kalnins–Miller transformations, J. Math. Anal. Appl. 324 (2006) 1152-1167.
generalizations of the Kalnins–Miller transformations, J. Math. Anal. Appl. 324 (2006) 1152-1167.
Z.Z. Zhang and M.X. Liu, Applications of operator identities to the multiple q-binomial
theorem and q-Gauss summation theorem, Discrete Math. 306 (2006) 1424-1437.
Z.Z. Zhang and J.S. Pang, Several q-series identities related to Jackson's,
Ars Combin. 102 (2011) 139-145.
Z.Z. Zhang and J. Wang, Two operator identities and their applications to terminating basic hypergeometric series and
q-integrals,
J. Math. Anal. Appl. 312 (2005) 653-665.
Z.Z. Zhang and T.Z. Wang, Operator identities involving the bivariate Rogers–Szegö polynomials and their applications to the multiple
q-series identities,
J. Math. Anal. Appl. 343 (2008) 884-903.
Z.Z. Zhang and J.Z. Yang, Several q-series identities from the Euler expansions of
_{\infty}) and
and
_{\infty}}) , Arch. Math. (Brno) 45 (2009) 47-58.
, Arch. Math. (Brno) 45 (2009) 47-58.
Z.Z. Zhang and J.Z. Yang, On two identities of Fu and Lascoux, Adv. Stud. Contemp. Math. (Kyungshang) 18 (2009) 59-67.
Y. Zhou and Q.M. Luo, Some new generating functions for q-Hahn polynomials, J. Appl. Math. 2014 (2014) Art. ID 419365, 5 pp.
J.-M. Zhu, The solutions of four q -functional equations, arXiv:1001.0299.
房剑平, q-微分算子恒等式的应用, 华东师范大学学报 (自然科学版) (2008) 20-24.
张之正, 杨继真, 双参数有限 q 指数算子及其应用, 数学学报 53 (2010) 1007-1018.
H.W.J. Zhang,
(q,c)-Derivative operator and its applications,
Adv. in Appl. Math.
121 (2020) 102081.