W.Y.C. Chen and R. Stanley,
Derangements on the n-cube,
Discrete Math. 115 (1993) 65-75.

Cited by

  1. C.G. Bailey and J.S. Oliveira, Enumerating the derangements an n-cube via Möbius inversion, arXiv:0902.0937.

  2. S. Bajnok and S. Shahriari, Long symmetric chains in the Boolean lattice, J. Combin. Theory Ser. A 75 (1996) 44-54.

  3. W.Y.C. Chen, Induced cycle structures of the hyperoctahedral group, SIAM J. Discrete Math. 6 (1993) 353-362.

  4. W.Y.C. Chen, G.Z. Gong and J.J.F. Guo, The sorting index and permutation codes, Adv. in Appl. Math. 50(3) (2013) 367-389.

  5. W.Y.C. Chen and P.L. Guo, Equivalence classes of full-dimensional 0/1-polytopes with many vertices, Discrete Comput. Geom. 52 (2014) 630-662.

  6. W.Y.C. Chen and J.D. Louck, Necklaces, MSS sequences, and DNA sequences, Adv. in Appl. Math. 18(1) (1997) 18-32.

  7. L. Cusick, Finite groups of derangements on the n-cube, Ars Combin. 116 (2014) 289-302.

  8. L. Cusick and O. Vega, Finite Groups of Derangements on the n-Cube II, Electron. J. Combin. 18 (2011) Paper 196, 6 pp.

  9. E.A. Donovan, Various parameters of subgraphs and supergraphs of the hypercube, Ph.D. Thesis, Northeastern University, 2009.

  10. J. Dybizbański and A. Szepietowski, Hamiltonian paths in hypercubes with local traps, Information Sciences 375 (2017) 258-270.

  11. J. Dybizbański and A. Szepietowski, Hamiltonian cycles in hypercubes with faulty edges, arXiv:1803.00064.

  12. M.R. Emamy-K., A geometric connection to threshold logic via cubical lattices, Ann. Oper. Res. 188 (2011) 141-153.

  13. M.R. Emamy-K., Cubical rectangles and rectangular lattices, arXiv:1803.10667.

  14. S.-P. Eu, Y.-H. Lo and T.-L. Wong, The sorting index and set-valued joint equidistributions of 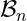and 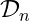, arXiv:1403.2169.

  15. N.J.Y. Fan, L. He, T.X.S. Li and A.F.Y. Zhao, The sorting index and inversion number on order ideals of permutation groups, Discrete Math. 339 (2016) 2490-2499.

  16. G. Gordon and E. Mcmahon, Moving faces to other places: Facet derangements, Amer. Math. Monthly 117 (2010) 865-880.

  17. J.R. Griggs, Rota's impact on matching theory and cubical lattices, In: Gian-Carlo Rota on Combinatorics, 572-580, Contemp. Mathematicians, Birkhäuser Boston, Boston, MA, 1995.

  18. C.M. Harden and D.B. Penman, Fixed point polynomials of permutation groups, Electron. J. Combin. 20(2) (2013) Paper 26, 23 pp.

  19. A. Ocneanu, On the inner structure of a permutation: Bicolored partitions and Eulerians, trees and primitives, arXiv:1304.1263.

  20. M. Ramras, Congestion-free optimal routings of hypercube automorphisms, SIAM J. Discrete Math. 10 (1997) 201-208.

  21. V. Reiner, Signed permutation statistics and cycle type, European J. Combin. 14 (1993) 569-579.

  22. B. Zgrablic, On quasiabelian Cayley graphs and graphical doubly regular representations, Discrete Math. 244 (2002) 495-519.