|
Abstract:
Let Sn denote the symmetric group on {1, 2,..., n}. For two permutations u, v ∈ Sn
such that u ≤ v in the Bruhat order, let Ru,v(q) and 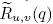 denote the Kazhdan-Lusztig R-polynomial and denote the Kazhdan-Lusztig R-polynomial and 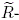 polynomial, respectively. Let vn = 34···n12, and let σ be a permutation
such that σ ≤ vn. We obtain a formula for the polynomial, respectively. Let vn = 34···n12, and let σ be a permutation
such that σ ≤ vn. We obtain a formula for the 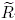 -polynomials -polynomials 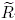 σ,vn(q) in terms of the q-Fibonacci numbers depending on a parameter determined by the reduced expression of
σ. When σ is the identity e, this reduces to a formula obtained by Pagliacci. In another
direction, we obtain a formula for the σ,vn(q) in terms of the q-Fibonacci numbers depending on a parameter determined by the reduced expression of
σ. When σ is the identity e, this reduces to a formula obtained by Pagliacci. In another
direction, we obtain a formula for the 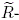 polynomial polynomial 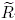 e, vn,i(q), where vn,i = 34···in(i +
1)···(n - 1)12. In a more general context, we conjecture that for any two permutations
σ, τ ∈ Sn such that σ ≤ τ ≤ vn, the e, vn,i(q), where vn,i = 34···in(i +
1)···(n - 1)12. In a more general context, we conjecture that for any two permutations
σ, τ ∈ Sn such that σ ≤ τ ≤ vn, the 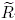 -polynomial -polynomial 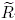 σ,τ(q) can be expressed as a product of q-Fibonacci numbers multiplied by a power of q. σ,τ(q) can be expressed as a product of q-Fibonacci numbers multiplied by a power of q.
AMS Classification: 05E15, 20F55
Keywords: Kazhdan-Lusztig R-polynomial, q-Fibonacci number, symmetric group
Download: pdf
|